Gabeland

I thought of this as a potential math competition problem, but I think it’s better if I share it here!
Consider the following setup:
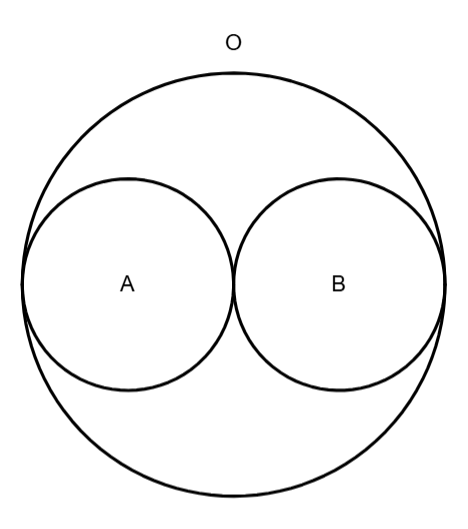
You have a circle of radius 1. Call it O. Two other circles of radius 1/2, A and B, are internally tangent to O and externally tangent to each other, like so:

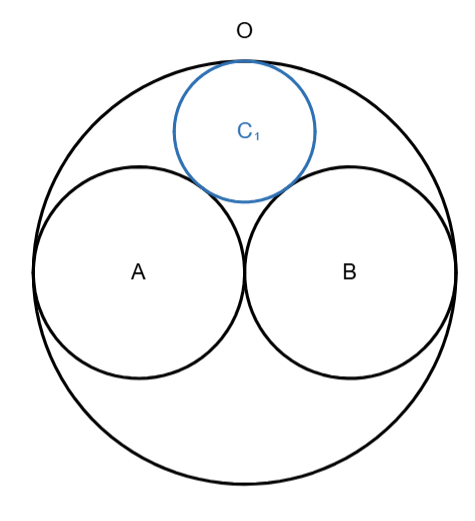
Now, C₁ is the circle that is internally tangent to O, but externally tangent to both A and B. There’s actually two of them, so I’ll just pick the top one.

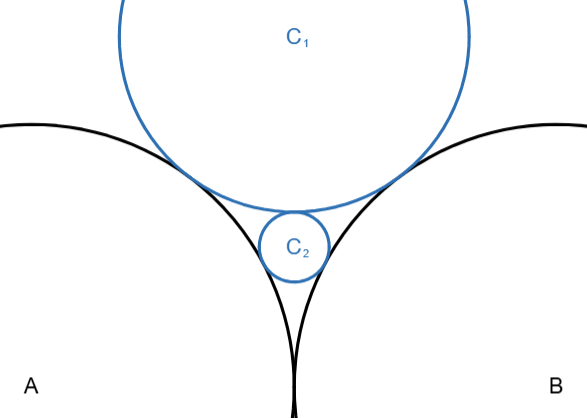
Next, C₂ is the circle that’s externally tangent to A, B, and C₁. This time there is only one.

I think you can see where this is going.

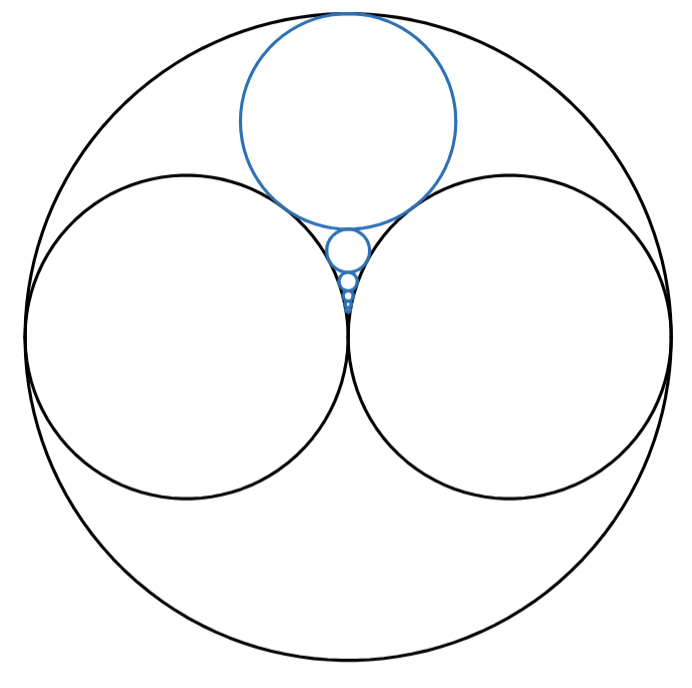
Each successive Cₙ (other than the first) is tangent to A, B, and Cₙ₋₁.
Now, here’s the question: What is the radius of C₁₀? How would you even figure that out?

The key to this problem is circular reflection.
Suppose we’re reflecting across a unit circle. To reflect a point, keep the angle the same but reciprocate the distance from the center, like so:

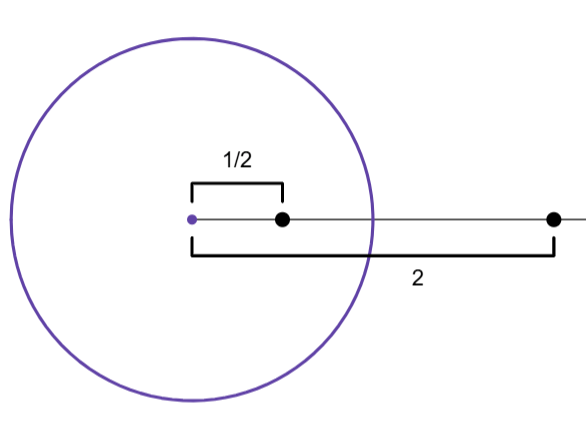
An interesting fact about circular reflection is that circles and lines always reflect to other circles and lines. For this, lines are effectively circles that intersect the “point at infinity”, so lines reflect to circles intersecting the center, as that reflects to the “point at infinity”. (1/0 = ∞?)

Here are some examples:

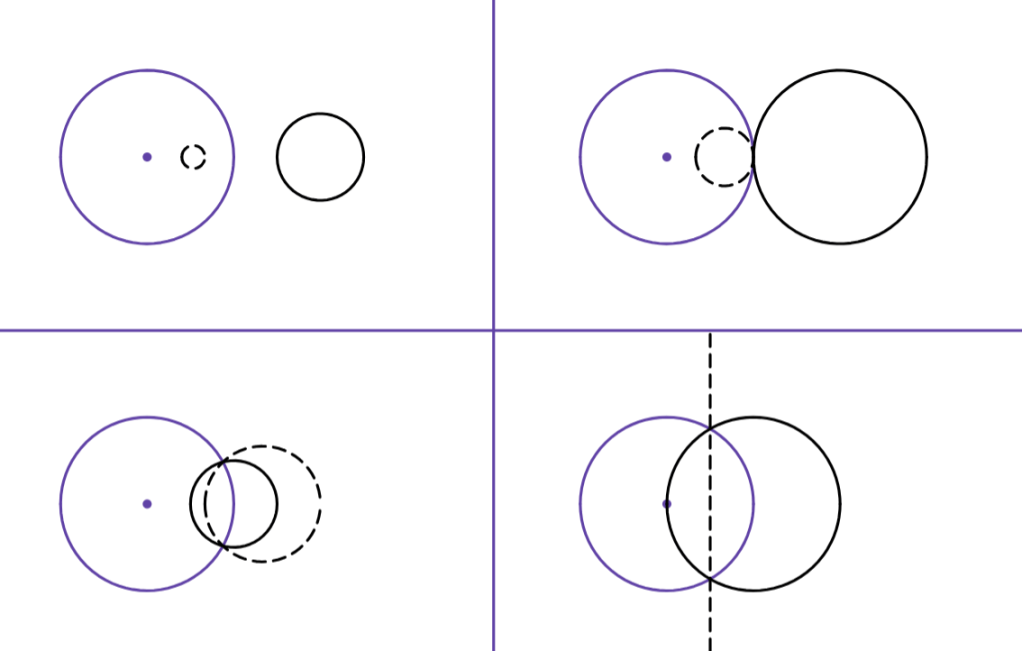
How does that help with the problem? Well, let’s reflect it and find out!

Let’s reflect across O. That seems the most natural.
With that in mind, what does A map to? It’s tangent to the circle on the left side, so that stays (points on the circle don’t change), and it touches the center, meaning it’s a line. There’s only really 1 possibility for that, then. And B is the same, just on the other side.

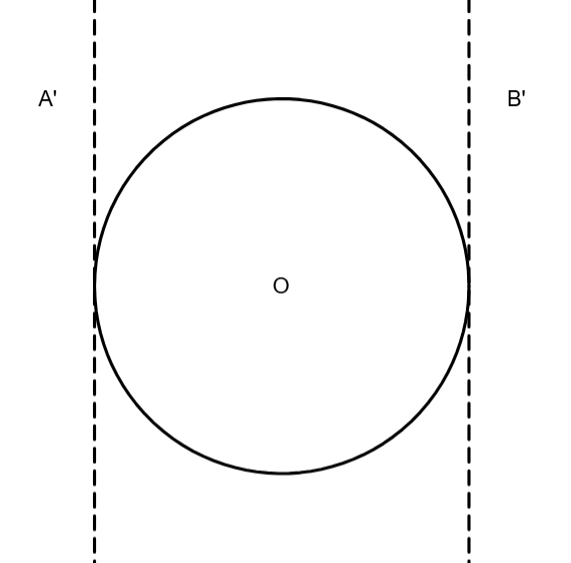
How about C₁? It’s tangent to O, A, and B, so C₁’ should be tangent to O, A’, and B’.

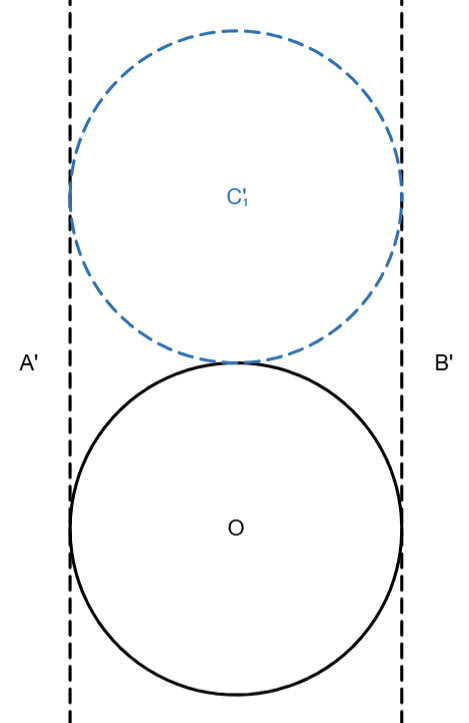
And C₂ is tangent to C₁, A, and B, so C₂’ is tangent to C₁’, A’, and B’.

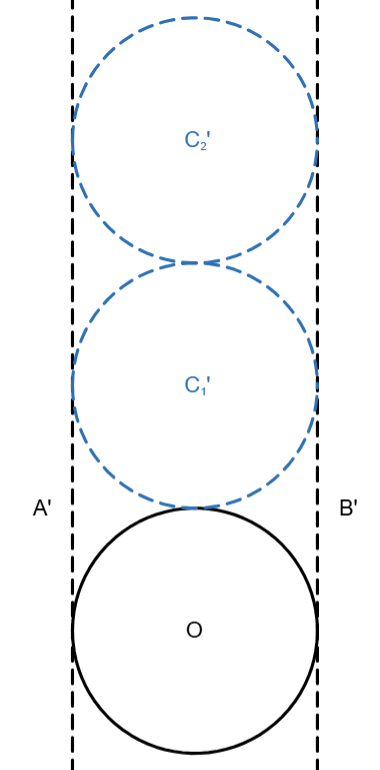
Let’s continue this all the way to C₁₀.

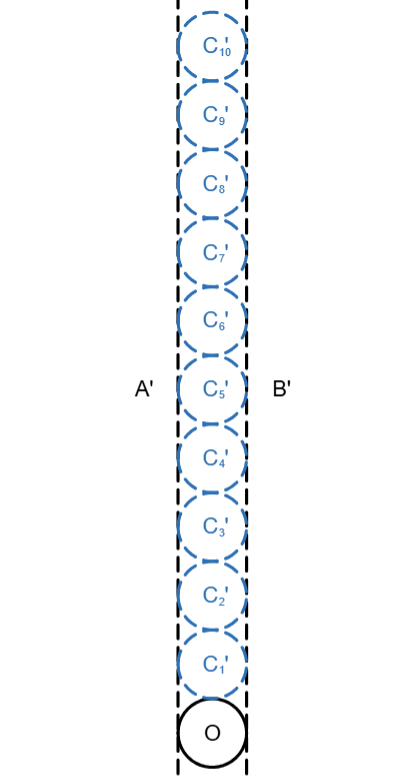
But how does this help with finding the radius? Well, now we can find the coordinates of the points of tangency.
The point between O and C₁’ is (0,1). The point between C₁’ and C₂’ is (0,3). The point between C₂’ and C₃’ is (0,5).
But, go back to the first two. If you go back to the un-reflected version,

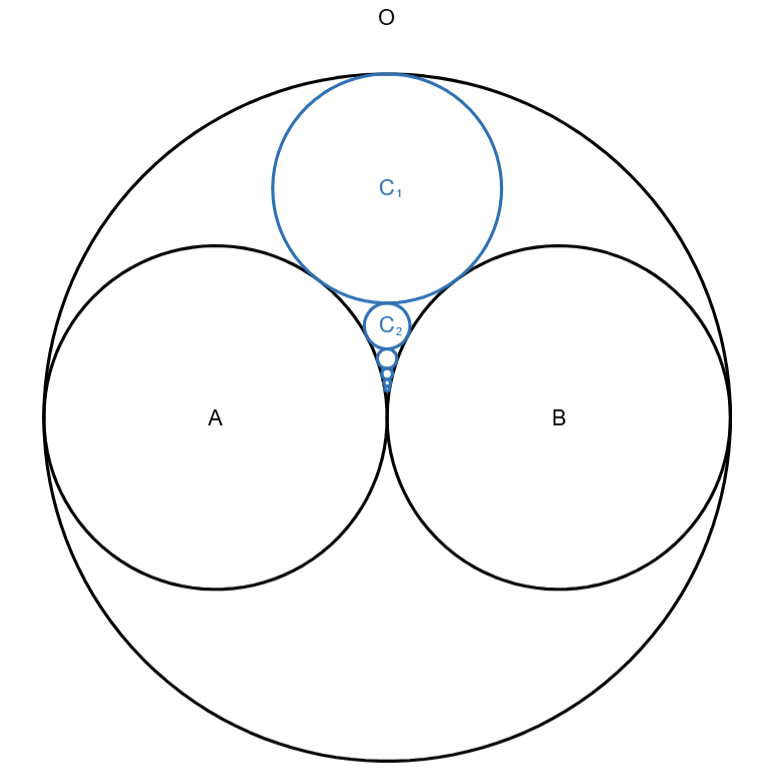
the point between O and C₁ is still (0,1), of course. But the point between C₁ and C₂ is (0,1/3).
That means the diameter of C₁ is 1-1/3 = 2/3, so the radius is 1/3.
Likewise, the diameter of C₂ is 1/3-1/5 = 2/15, so the radius is 1/15.
That gives us exactly what we need to figure out the radius of C₁₀.
The point between C₉’ and C₁₀’ is (0,19), so the point between C₉ and C₁₀ is (0,1/19).
And the point between C₁₀’ and C₁₁’ is (0,21), so the point between C₁₀ and C₁₁ is (0,1/21).
So the diameter is 1/19-1/21 = 2/399, and the radius is 1/399.

How would anyone ever think of that? They wouldn’t. And that’s why this isn’t actually a math competition question.

(P.S. I’m starting a schedule. I’ll try to make one post each week, on Saturdays.)